内容摘要:

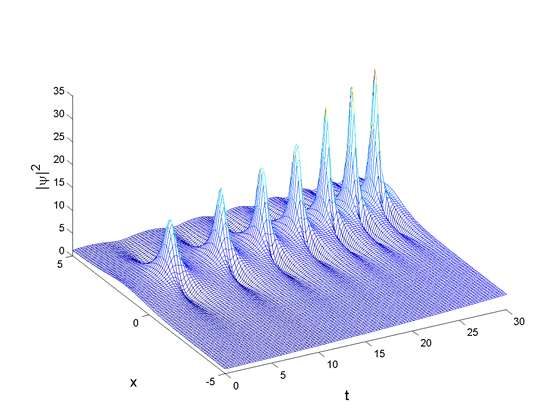
　 　玻色－爱因斯坦凝聚在分子场理论框架下可以用Gross-Pitaevskii方程描述，并在一定条件下可以化为一维非线性薛定谔方程。但至今仅标准非 线性薛定谔方程可以严格求解。获得不同类型的非线性薛定谔方程的严格解对研究和深入了解玻色－爱因斯坦凝聚的行为具有非常重要的意义。梁兆新、张志东和刘 伍明合作研究给出了一个一维非线性薛定谔方程的严格解，它描述了在一个排斥势中随时间变化的原子间相互作用的玻色-爱因斯坦凝聚的一个亮孤子的动力学。发 现在亮孤子中的原子数可以保持一个动力学平衡：在亮孤子和背景间存在一个时间周期的原子的交换。结果表明，在一定的参数范围内，亮孤子可以通过增加原子的 散射长度被挤压成非常高的局域物质密度。这提供了一个实验的工具来确认一维Gross-Pitaevskii方程的适合应用的范围，并可以实现对玻色-爱 因斯坦凝聚态的挤压与控制。由于一维非线性薛定谔方程还可以描述光子晶体、光纤通信、磁性孤立子等许多物理系统的非线性动力学行为，因此这项研究结果对这 些研究领域也将有很大的启迪。

 Phys. Rev. Lett. 94 (2005) 05040